The generalized first law and thermodynamic cycles

by W.D. Bauer ©, released 7.12.99, corrected 16.10.01, 06.03.02

Abstract:
It is shown that the generalized first law holds as a mathematical relation for reproducible physical exchange processes of additive quantities. It can be applied as a definition tool even if the balances can not followed experimentally. As an example a Bender equation of state for multicomponent mixtures was calculated in a centrifugal field.
 

1. Introduction

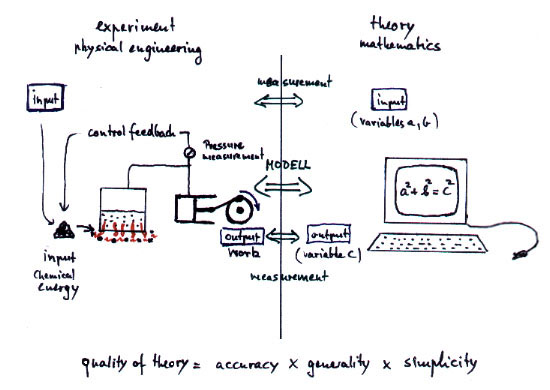
The essence of physics consists in the mapping of real processes to theoretical mathematical models which should show quantitatively the same features as found in reality. By defining a physical measurement the variables in the theory are connected to the physical reality. If the concerning variables of the theory coincide quantitatively with the real measurements then we say the theory is correct, comp. fig.1.
Acc. to Newton physics is obliged to the principle of "hypotheses non fingo", i.e. the implementation of physically (or psychologically) motivated principles as mathematical constraints of a theory should be avoided because this entrains a loss of generality and the danger of arising inconsistencies. Nevermind, sometimes it is done for tentative purposes,  and sometimes this strategy even seems to yield correct predictions. However, if such heuristically motivated constraints cannot not be founded in a more general framework with time they survive sometimes as "natural laws" for centuries because their preliminary heuristic character is forgotten. They are vulgarized, overgeneralized, are combined with economic interests and exert a considerable suggestive blocking pressure on learning people.
"Natural laws" are not made by god but by a man fitting the mapping of a mathematical theory to the experimental reality using the term "natural law" as power amplifier for selling his products and opinions . In reality any physical description is a compromise between what we can see and what we want to see. And what we want to see is determined by our social, economic, moral, religious and instinct motivated prepolarisation which sets up our projections on that what we regard to be the reality.
Due to such psychologically motivated reasons misinterpretations oftenly apply especially to the fundamental laws of physics like the first and second law. Therefore, we start our article with very simple and banal mathematical ideas.
 

2. The generalized first law

2.1 Definition of a machine
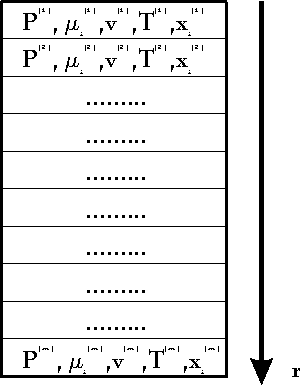
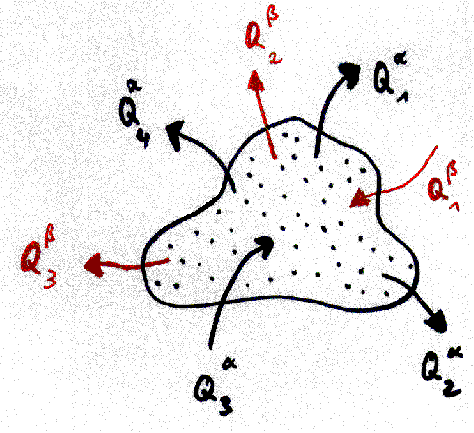
We define a machine as a coherent volume of space which exchanges one or more different qualities of quantities with its environment (for instance mass, energy, angular momentum). The volume of the machine (or the system border) can change as well. We demand that the volume change and all exchange processes with environment can be done periodically. 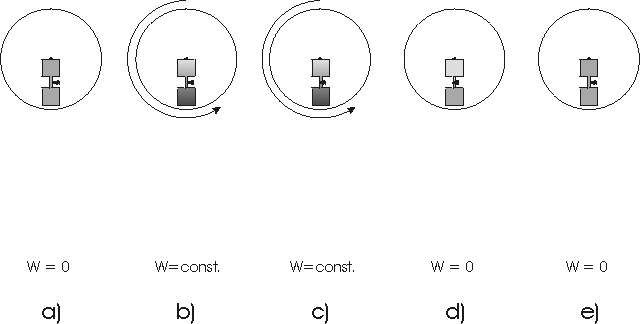We may or may not know what happens in the inner of the machine. A simple scetch of a machine can be found in fig. 2. It is clear that this definition extends not only to conventional machines but to many physical processes as well, comp.[1,2]
 

2.2 The generalized first law
Physical processes are described normally by differential equations. These can have relaxing, exploding or periodic solutions. Otherwise, strange attractors or complete chaotic solutions are possible. It is clear that a machine has to be able to work periodically or -if we use a physical term- reproducible which means that the machine process can be done periodically.
The coordinate of the exchanging qualities has to be localized uniquely, i.e. in- or outside of the machine. This means: the qualities are deterministic, i.e. uniquely defined in space und time. The quantities can cross the border between the machine and environment. With these concepts in mind we can formulate "our" generalized first law

Proposition:

We have
1) a machine, which works reproducible
2) an exchange of qualities Qi with the machine, which are additive and deterministic
then the generalized first law means:
After a cycle of the machine the in- and effluxes kQi of the qualities Qi are zero

Proof:
Due to reproducibility the machine contains the same amount of each quality Qi after a complete cycle time  T as before starting the cycle. Therefore, - due to the additivity -the sum of in- and effluxes of each qualitity Qi during the cycle must be zero as written down in the formula above.

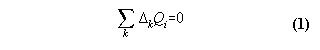
It is clear that a first law balance holds generally only after a cycle is performed completely. Sometimes special cases exist where the balance is fulfilled even from point to point of a cycle but it does not hold generally if only a part of the cycle is proceeded. An example for this is liquid water under 4 degree Celsius. If we take off heat from it by cooling it down it expands and performs work. In sum we get heat dQ and work dW by doing this process from A to B. The energy balance dQ +dW =0 is fulfilled only after a complete cycle is proceeded and the substance comes back to the initial starting point of the cycle.
After many cycles the impression appears that the quantities are conserved because the mean of the total balance is conserved in the mean if time goes to infinity.
In order to apply the first law correctly we have to find out the range of validity of the above assumptions for each qualitity Qi. It is clear that the proposition can not cover quantum mechanically defined quantities because these are deterministic only for limit cases. Furthermore, it is critical to apply it to irreversible non-reproducible processes, because it is hardly possible to prove anything under irreproducible conditions.
If concreticized the qualities Qi can be energy, charge, mass, momentum and angular momentum. The applicability and the consequences of the above proposition will be discussed for each of these qualities in the next sections.
 

2.3. The first law applied for the quality of energy
In classical physics the quality energy E is defined generally by the equation

or in terms of energy densities
Realizations of the generalized abstracted entities f and x can be found in tab.1. Any working cycle can be represented in a f-x - diagram, the work is represented by the area, the orientation says whether energy is taken up or set free, see fig.3 a) and b).
If a machine process exchanges energy of different qualities in a complete cycle of duration T the first law is
This means that all generalized forces fi of the cycle can be derived from a potential function U(xi) by
Special cases and definitions:
1) If U is dependent only from x, but not from derivatives of x or from time t, then we have a equation of state. Otherwise, the potential holds only for a special parametrisation of the cycle.
2) If a energy balance which has only two terms we call it a conversion. It describes the interchange of one form of energy in another. The mechanic energy balance of the harmonic oscillator is an example for such a case. It describes the permanent exchange between kinetic and potential energy. Here furthermore, the special case of energy conservation of U from point to point of a cycle is realized.
Another well known example is the conversion from work into heat by friction losses by a brake. A further example can be extracted as a special case from the Poynting "energy conservation law" which describes the conversion from electrical current into magnetic or electric field energy vice versa if we neglect the radiation term. The proof can be found in appendix 1.
3) If the energy balance has more terms than two then one form of energy can be regarded as the "currency" of the cycle by which all others forms of energy are interchanged. In an electric motor the "currency" is the magnetic field by which motor energy, heat losses and electrical power are exchanged. In an electric network the electrical power can be regarded as currency by which the chemical energy of the battery and the heat losses of resistors are exchanged.

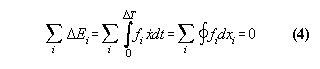
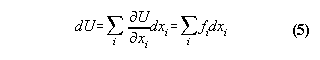
Examples:
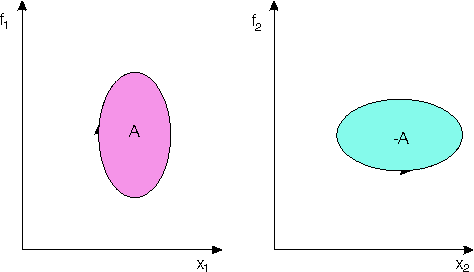
1) Conservative systems
If we make concrete x and f with

then the differential above can be identified with usual standard thermodynamics formalism
2) Non-conservative (and dynamic) systems
We will consider here a water and a wind wheel and discuss three simple cases:
a) water wheel totally merged in flowing water field, comp. fig.4a)
The force on the paddle is defined by f~v.A.cos. Because the velocity field v is laminar and conservative, the resulting force field is conservative as well due to the coupling A.cos. Therefore no energy will be given off after a cycle. The driving force field is conservative, i.e. a subspace of the space described by the vector fi is conservative as well. The wheel will not not turn.
b) water wheel with lower half in a constant flowing water field, comp. fig.4b)
In this case the driving field is non-conservative and the wheel will turn.
c) wind wheel in a constant laminar wind field, comp. fig.4c)
In this case the field v is conservative but due to the locally dependent coupling of the force to the v-field by the paddles, the force field itself is non-conservative. Therefore, field energy is taken out of the field and changed into mechanical energy. The wheel will turn.

All these examples seem to look quite trivial, however if we change the meaning of the variables in examples of figures 4 we can easily find analog systems which appear to be perpetuum mobiles of first kind, comp. tab.2 showing these analogies. For instance, if we postulate a "strange" magnetic material coupling to a conservative magnetic field then we can get running a magnetizable bowl on a circular track in a magnetic field as shown in [3]. Here, acc. to the theory field energy tapped is changed into work even if no "influx of magnetic energy" can be detected from outside. Similarly, if we have (electric or magnetic) capacitive material properties, which change parametrically in time, analogous "overunity" effects are principally possible as well.[3]
In sum, we can conclude: Regardless, whether energy in- or effluxes of a machine can be found experimentally or not, a balance hold for every system under description. The "first law" is used as a mathematical tool to calculate and to describe cycles: This means, all machines including perpetuum mobiles of first kind fulfill the first law per definition !
 

2.4 The first law applied for the quality of mass
It is quite trivial that mass is an additive quantity. It should be mentioned that -similarly for energy- this does not hold for relativistic cases because then mass and energy cannot considered separately. In this article such problems are not followed.

2.5 The first law applied for the quality of charge
As well as mass charge is an additive quantity and this hold even for the theory of relativity.

2.6 The first law applied for the quality of momentum
Momentum is regarded as a conserved quantity in the common sense of any physicist. However, critical examination shows that it is appropriate to be more careful with this assumption. Generally, momentum is not conserved for any system, whose Lagrangian is dependent not only from a velocity coordinate but from a space coordinate as well. Momentum conservation means always a special case of the equation of motion, i.e.

Therefore, the potential V(r) has to be constant for energy conservation because L = T - V with T=p2i /2mi . Similarly constraints can destroy momentum conservation as well for more particle systems. An example demonstrating this for angular momentum is given in [3]. There it is shown that a conserved quantity can be found which is not the total angular momentum of the system, comp.fig 5. Further examples for other mathematically conserved quantities deviating from simple physical terms like energy of the system, momentum ect., can be found in a standard textbooks [4] or in [22].
An example demonstrating the dependence from the choice of the coordinate system is shown in fig.6a and b). In case a) we have a planetary two body problem, whose common center of mass is the origin of the coordinate system. Here, the total momentum is conserved. In b) We have the analog electric problem. Here the center of rotation is fixed to the ground with the cental body. The momentum is not conserved. The difference is due to the different chosen system border of the system which can be done arbitrarily. Therefore, by arbitrary choice of the physical system and its mathematical description we "generate" the "nature laws" which we want to see.
There exist references which calculate the total momentum balances for machines (valid from point to point) quite generally [1]. The range of validity in this article [1] is restricted to free particle systems however it can be extended to equivalent particle systems whose inner forces are central forces, i.e. forces on the connection line dependent only on the distance between the particles as shown in appendix 2. Electromagnetic fields are not contained in the cited reference.
Furthermore, acc. to this reference all (mechanical) momentum exchange between the system and the environment should be measurable acc. to
which means point to point conservation of momentum.
Acc. to our first law the idea of balances can be generalized for cycles where momentum balance is not apparent or measurable from point to point. Due to the reproducibility of the system we can write down a momentum potential difference UP for a cycle
where the pki are the momenta of different particle i of the different qualities indexed by k. Then, point to point balance equations can be derived from such expressions as a special case.
 

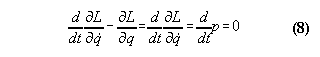
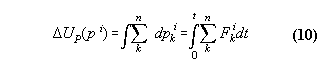
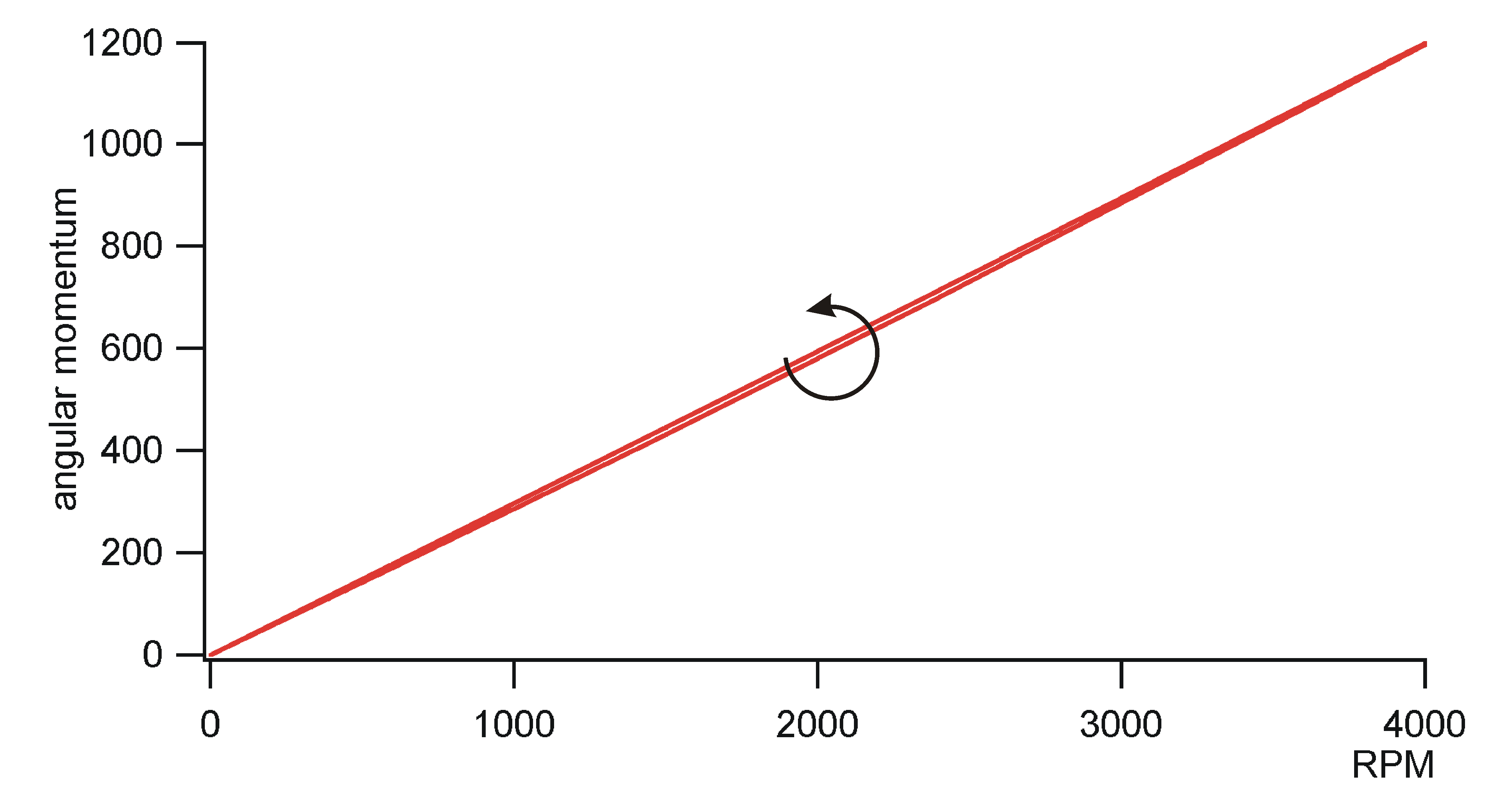
2.7 The first law applied for the quality of angular momentum
It is clear that analogous considerations like that of the last section should be possible for angular momentum. Consequently, it should exist an angular moment balance, an angular moment potential for cyclic processes for periodic machines. However, the author did not find balance equations of angular momentum in literature at first sight. The cause of that may be that the standard definition of angular momentum is not appropriate for a many particle system. The standard definition of angular momentum is

It presumes the additional knowledge of a preferred rotation axis point. The definition is not independent from the choice of the coordinate system. Even a linear motion has a angular moment dependent from the origin if we define an axis point at anywhere in space. Therefore, it is appropriate to try to give a definition of angular moment for a general moment distribution of particles, which we define by
where r0  is the center of mass of the distribution and  is the mean of the momentum distribution. This definition has the advantage that angular moment independent from the choice of the coordinate system as shown in fig.7. It is a measure of the non-collinearity of a momentum distribution. The definition is only a first idea. Its usefulness has still to be tested out.
 

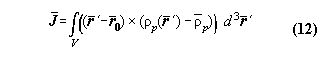
3. A cycle with fluids in a field

3.1 Previous works
The idea that cycles binary mixtures in fields may violate the second law was due to B. van Platen who became known as the inventor of adsorption refrigerator[5]. A. Serogodsky made measurement on a similar cycle and claimed to have measured such violations. Calculations with a modern equation of state  without fields did not confirm any claim of both [6,7]. These claims were tested out using two possible axiomatizations of thermodynamics. The first axiomatization was based on the conventional Sears-Kestin version of the second law which forbids per dogma any equation of state which give such "strange"solutions. The other "axiomatization" was based on the extremum principle of the potentials. The second possibility is only apparent but not really an axiomatization of thermodynamics because it can be motivated by a derivation of thermodynamics from mechanics [8]. It has the advantage that it reduces the number of hypotheses. No additional "physical axiom" like second law based on experience or overgeneralization (dependent from your personal point of view) is necessary. The alternative axiomatization derives the second law as a consequence of the mathematics of the system. It allows the second law to reverse if fields are present as shown in [9]. Acc. to [6,7], both axiomatizations yield no second law violation for calculation of a van Platen or Serogodsky cycle using a equation of state (EOS).
Therefore, in order to test out the van Platen claim completely it is necessary to include the dependence from the field whose influence can be significantly in the neighborhood of critical points. The idea  is near to use space-dependent thermodynamics including fields to test out the equation of state behavior in fields as proposed indirectly already in van Platen's patent.
A formal similar problem (but more simple 2-variable system independent from any space coordinate) has been discussed recently by the author. This model of a polymer solution system describes phase transitions in an electric field. It is confirmed qualitatively in parts by experiments[11]. Consequent application of this model predicts overunity behavior due to "irreversibilites in the other direction" which are possible if one accepts the our interpretation of second law[7].
By applying analogous considerations to other potential fields it is possible to enlarge the number of possible candidates for second law violations. In tab. 2 we give an overview of some possible fields which allow such cycles. In appendix 3 the second variation of the least action functional is derived for gravitation and centrifugal fields indicating the possibility 2nd law violating cycles.
 

3.2 General formalism of space dependent equilibrium thermodynamics including potential fields

3.2.1 General thermodynamic theory
It is well known that any static thermodynamic material property can be described generally by a potential like inner energy U(S,V,ni) or G(P,T,ni) chosen acc. to the problem under question.
If fields are taken into account, the thermodynamic equations become dependent from the (here one-dimensional) space coordinate r additionally . Then, the ansatz of inner energy U* in field can be written [8]

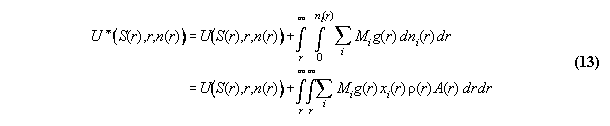
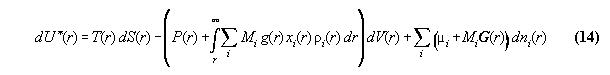
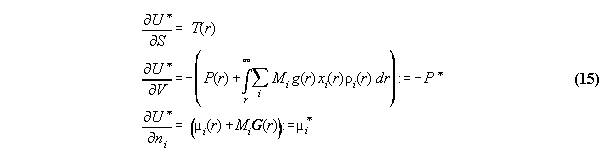
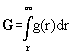with the definitions U* :=total inner energy, U:=inner energy without field , Mi:=molecular weight, xi:=molar ratio of species i, (r)=1/v(r):=molar density, A(r):=cross section of volume at r and g(r):=gravitation field . Therefrom, the total differential of U* is derived as
with the Maxwell relations
Here, we used the definitions P(r) := measurable barometric pressure at r,  := gravitational potential and dV:=A.dr. We denote P* as the global total pressure (a fictive value without any physical observable relevance), which is constant and characterizes mathematically the global coupling over the whole volume. Similarly µi* is the global total chemical potential. This general formalism makes thermodynamics dependent from the space coordinate r of the field, it includes not only the description of barometric and hydrostatic pressure phenomena (if P* 0 [10]), but furthermore allows to calculate density and concentration profiles of fluids in fields. The formulas are surely not new and coincide with known derivations[12].
 
 

3.2.2 Phase equilibrium with field
Acc. to the standard Gibbs the variation the inner energy at a interface of two phases

has to be minimized to zero if dSli = -dSg , dV:=dVli = -dVg and dni:=dnili = -dnig are varied. Therefore we get
These equations hold locally at the interface r0 between the two phases (if we neglect surface energies).
In the one phase areas in fields, however, the equilibrium conditions
hold between adjacent space cell in the mixture. This is proved in the appendix 4 acc. to Gibbs's way of thinking.

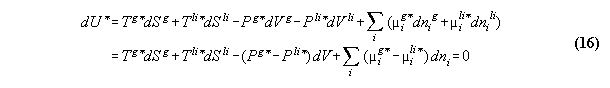
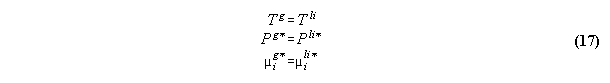
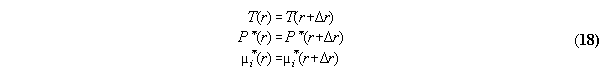
3.2.3 Conclusions
In general, if a field is present, pressure gradients are generated which induce as well concentration gradients in the volume. Therefore, phase equilibria differ from point to point along the field direction. At each point r of the volume, however, the local equilibrium state and the rate constants can be determined acc. to usual thermodynamics without field, if P(r),T, and xi(r) are known. Due to the global coupling in the volume, the equilibria shift in sum relatively to the uniform state without field, especially if
1) the molecular weights of the components are high
2) high pressure differences arise in the fluid due to a high field which induces high differences in the activities of the components as well, or
3) the local different barometric pressures in the system are in the neighbourhood of a critical point and even slight variation of parameters of P generated by the field can produce big variations in activities and densities of the fluid.

Furthermore, phase equilibria can depend from the shape of the vessel due to global coupling of the particle number over the whole volume. The dependence of the pressure profile depends from the form of the vessel i.e. the hydrostatic paradoxon fails to exist generally for multicomponent systems.
 

3.3 The computation of thermodynamic equilibrium of a mixture in a field with a equation of state

In the following we will describe how the general theory of the last section can be made concrete by a numerical solution of a phase equilibrium. We will describe subsequently the different program modules (or numeric functions) which - if built together - allow to calculate the phase equilibrium in a field.

3.3.1 The Bender equation of state- the subroutine EQOFSTATE
In order to get a good accuracy in our calculation we take a modern generalized Bender equation of state[14] which allows to calculate analytically for all thermodynamical properties and which can be programmed economically using the Horner sceme[14,15]. The equation has the form

with
where  with the subscript c indicating critical material constants. The  are defined by . The g-coefficients are tabulated in [14] or can be drawn here.  (acentric factor) and  (Stiel-factor) are material constants taken from [14, 15]. In order to calculate mixtures the critical material constants have to be made dependent from concentration. This is marked in the text below by the additional index M. We apply the pseudo critical mixture rules of Tsai and Shuy [16] in a version of Platzer[14].
,  and kij are fit constants improving the accuracy between measurements and formula description.
We propose additionally a new still untested mixture rule for powers characterizing material properties in ternary and higher component mixtures with appropriate chosen material constants Mix1ij and Mix2ij for each mixture
The material data of the pure components were taken from [14, 15] and [17] where more details for estimation of constitutive data of pure components can be found. In our program the equation of state is programmed in a subroutine called EQOFSTATE. This routine calculates the whole thermodynamic state if v, T and xi are given. Furthermore, it calculates derivatives necessary to determine phase equilibria. Details of the calculation can be found in appendix 5.

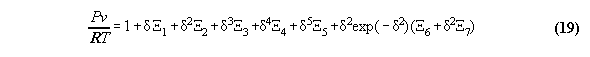
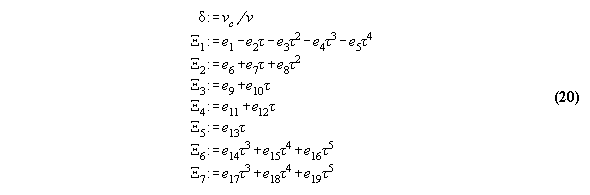
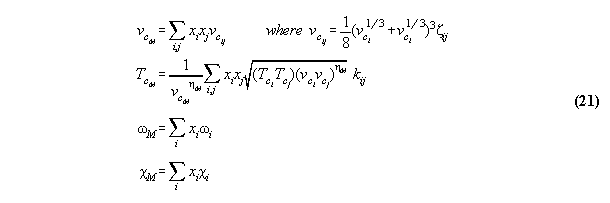
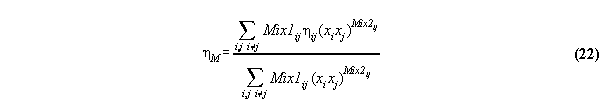
3.3.2 Calculation of phase equilibrium - the subroutine NEWTONGAUSS
In order to calculate the phase equilibrium the equations of the Gibbs fundamental system have to be solved. The first equation equals pressure in vapor and liquid

The other equations equal chemical potential or fugacity in vapor and liquid for each component. In our case we use the definition of fugacity, i.e.
where the fugacity coefficients are calculated acc. to a formula derived in [18] with ZM:=Pv/RT
Because -for a binary mixture- x1f and T are fixed variables and vf ,vg and x1g are wanted we get the equation system
which is solved using a standard Gauss-Newton or Newton-Raphson algorithm. Using the numerical solution all other thermodynamic quantities can be derived.

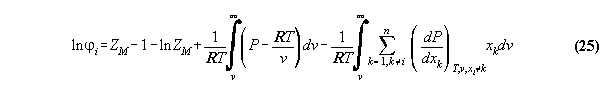
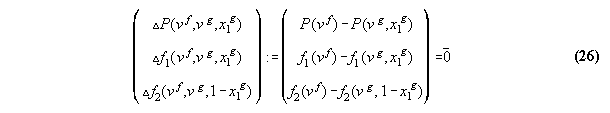
3.3.3 The inverted equation of state V(P,T,xi) - The subroutine V_PTX
The Bender equation of state is formulated analytically in the form P(v,T,xi) with v, T and xi as independent variables. For some purposes however (as we will see below) it is appropriate to have the same equation of state (EOS) in the form V(P,T,xi). If we want to know the thermodynamical state in dependence from P0, T and xi, the inversion is done numerically by solving the equation

P0 - P(v)=0
by a standard Newton-Raphson  algorithm. P0 is the preset pressure, P(v) is the Bender equation in dependence of v which is iterated until the accuracy is sufficient. The variables T and xi are dropped in our representation because they are constant during the iteration.

3.3.4 The thermodynamic state dependent from P and fi - the subroutine VX_PF
Because the inverted EOS is needed for the least square algorithm a subroutine has been to evaluate the EOS values dependent from P,T and xi. With T constant and skipped here such a set consists of equations for

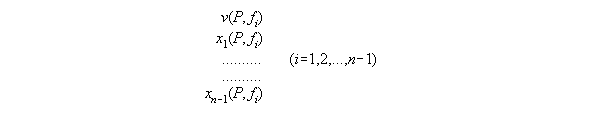
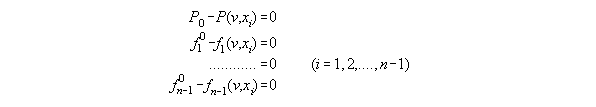
The numerical solution of this set can be obtained from the Bender equation of state by solving the system of equations
by a Newton-Raphson iteration procedure. P0 is the fixed pressure, fi0 are the fixed fugacities, P(v,xi) and fi(v,xi) are calculated by the Bender equation in dependence of the wanted values of v and xi which both are iterated until the accuracy is sufficient.

3.3.5 The thermodynamic statedependent from P and µi - the subroutine VTX_PMu
In order to calculate the compartment array of a fluid under a field it is appropriate to have the set of constitutive equations dependent from P and µi. Such a set consists of equations for

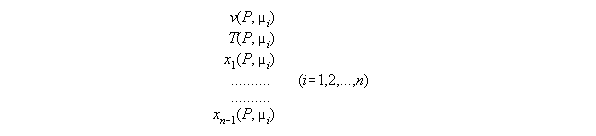
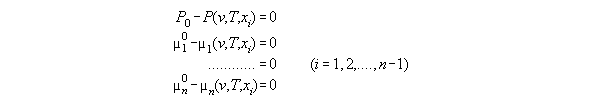
The numerical solution of this set can be obtained from the Bender equation of state by solving the system of equations
by a Newton-Raphson iteration procedure. P0 is the fixed pressure, µi0 are the fixed chemical potentials, P(v,T,xi) and µi(v,T,xi) are the calculated values from the Bender equation in dependence of the wanted values of v,T and xi which both are iterated until the accuracy is sufficient.

3.3.6 The volume array calculation in an arbitrary potential field- the subroutine VOLUME (Footnote)
If a field is applied pressures and chemical potentials differ from point to point. The subroutine VOLUME calculates the profiles of pressure, concentration and chemical potentials along the space coordinate of the known field if in one point of the volume P and xi are known. Our program calculates only one-dimensional profiles in a tubular housing,
Generalization to more dimensions and other forms of housings would be easily possible but is not done here. For calculation the whole volume is divided into a array of m equal subvolumes dV(rj ) (at same potential) at the space coordinate rj. At one point rref called reference point we assume to know the pressure P(rref) and the concentration xiref . Then, all other points in the volume are interconnected to their neighbor compartment by the equations for (hydrostatic) pressure using g(rj-1)=-dV(rj-1)/dr

and for chemical potential

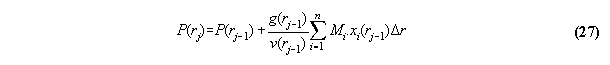
For concrete programming the formula µi=µi0(p+,T)+ RT ln(fi /p+) + Mi .V(r) has to be applied.
The subroutine sums up as well the total number Ni of each particle in the total volume because it is needed in the next subroutine. Therefore, the algorithm proceeds as follows :

1)  Define the number M of volume array cell, i.e. the partition of the volume .
2)  Give pressure P0, temperature T0 and concentrations xi at one point rref called the reference point
3)  Using the subroutine V_PX invert numerically the equation of state at rref and calculate v
4)  Initialize the particle numbers Ni=0
5)  FROM volume array cell J=1 TO M
6)      Determine all interesting thermodynamic data at rj using EQOFSTATE, especially µi and dni(rj),
          i.e. the number of particles of each sort i in this subsection dV(rj) of V
7)      Ni=Ni+dNi(rj ) Add up the particle number in the compartment to find the total number of the array
8)      Determine P and µi in the next adjacent volume section dVj+1 acc. to equations (27) + (28)
9)      Invert numerically the equation of state at rj+1 and calculate v,T,xi using the subroutine VTX_PMu
10) NEXT J
11) Give out all calculated values

3.3.7 Volume array calculation at conserved particle numbers - the subroutine N_PX
Because the total particle number is conserved in the most problems, the volume array in the field has to determined under the constraint Ni0=consti. Acc. to the last section 3.3.6 the total particle numbers Ni in the volume is calculated in the subroutine VOLUME . This numbers can be regarded as numerical functions of the starting values Pref and xiref in VOLUME , i.e.

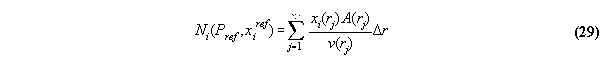
Because we fix the number of particles in our problem the functions have to be numerically inverted in order to find the correct starting values Pref and xiref for the subroutine VOLUME. This can be done by solving numerically the equation system
by a Newton-Raphson algorithm. Here all the derivatives of the Jacobimatrix has to be determined numerically. After the iteration is completed the subroutine VOLUME calculates the complete thermodynamical state of the volume array.

3.3.8 Fitting generalized Bender equation to empirical mixture data -the subroutine LEASTSQUARES
Because only few published unreliable fit parameter exist for mixtures calculated using the Bender equation, the fit constants must be calculated from empirical data. Therefore, a known least square fit algorithm [19] and [20] was  implemented in a subroutine LEASTSQUARES. This sub-routine fits the parameter kij,  and  to empirical values. The input of this routine contains the starting values of the fit constants, experimental values, fixed parameters like material constants, allowed errors and switches used for economical programming. The output of this routine consists of the results of the iteration, i.e. the fit constants and furthermore the least squares sum values and errors documenting the performance of the iteration. For a critical discussion of the fit method and its results click here .
 

4. Results

We used Argon-Methan data [21] to test our algorithm. The choice of this system was due to wrong expectation disproved in the course of the investigations and was continued then as lab rat for study. For practical purposes under environment conditions, mixtures of Nitrogen, Argon, SF4, SF6 as superheated component and Propane, Butane, CO, CO2 as condensable component are possible. (We omit here the classical refrigerants.)
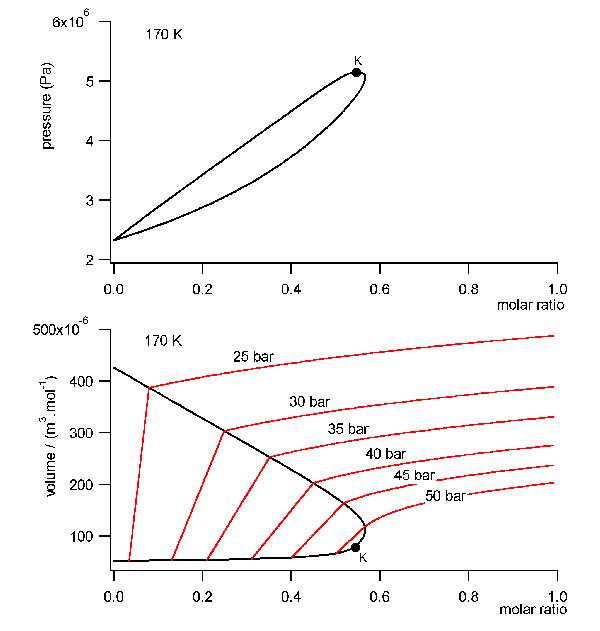
First, we calculated appropriate fit constants to the data using the least square routine. For results click here ! With these model data we calculated the rotator cycle. We choosed as field free initial state a mixture with a molar ratio of Argon of 56%, 55 bar and 170 K. This is very near in the neighborhood of the critical point in the gaseous ara of the phase diagram, comp. fig.8 . The rotator cycle is shown in fig.9. The closed volume of the mixture is set under rotation. At 4000 RPM the total volume is split unsymmetrically into two halves by a tap. The split point is chosen arbitrarily at the point where the specific volume in the field equals about the specific volume without field. Then, both volumes are decelerated again to the field free situation. 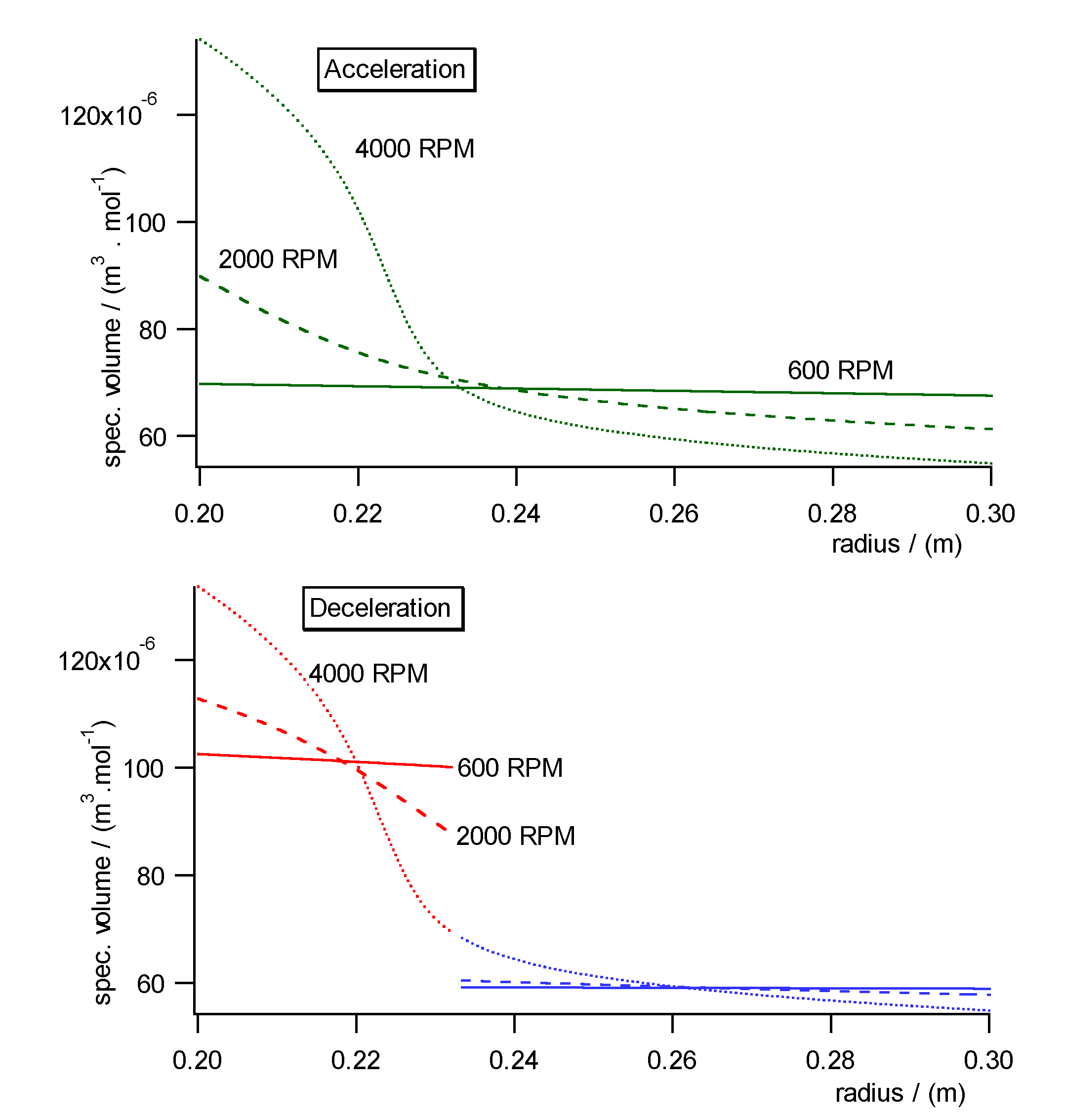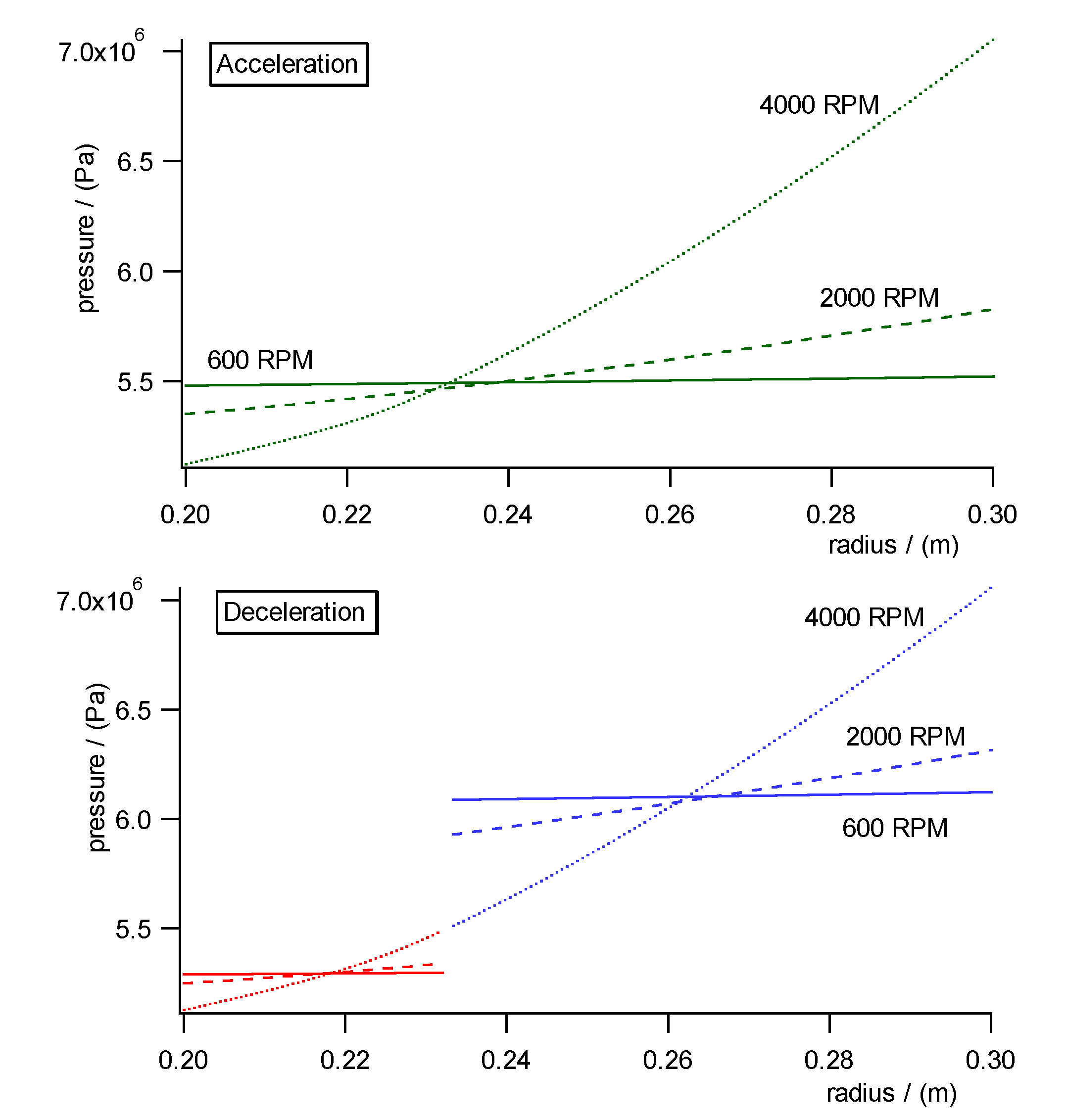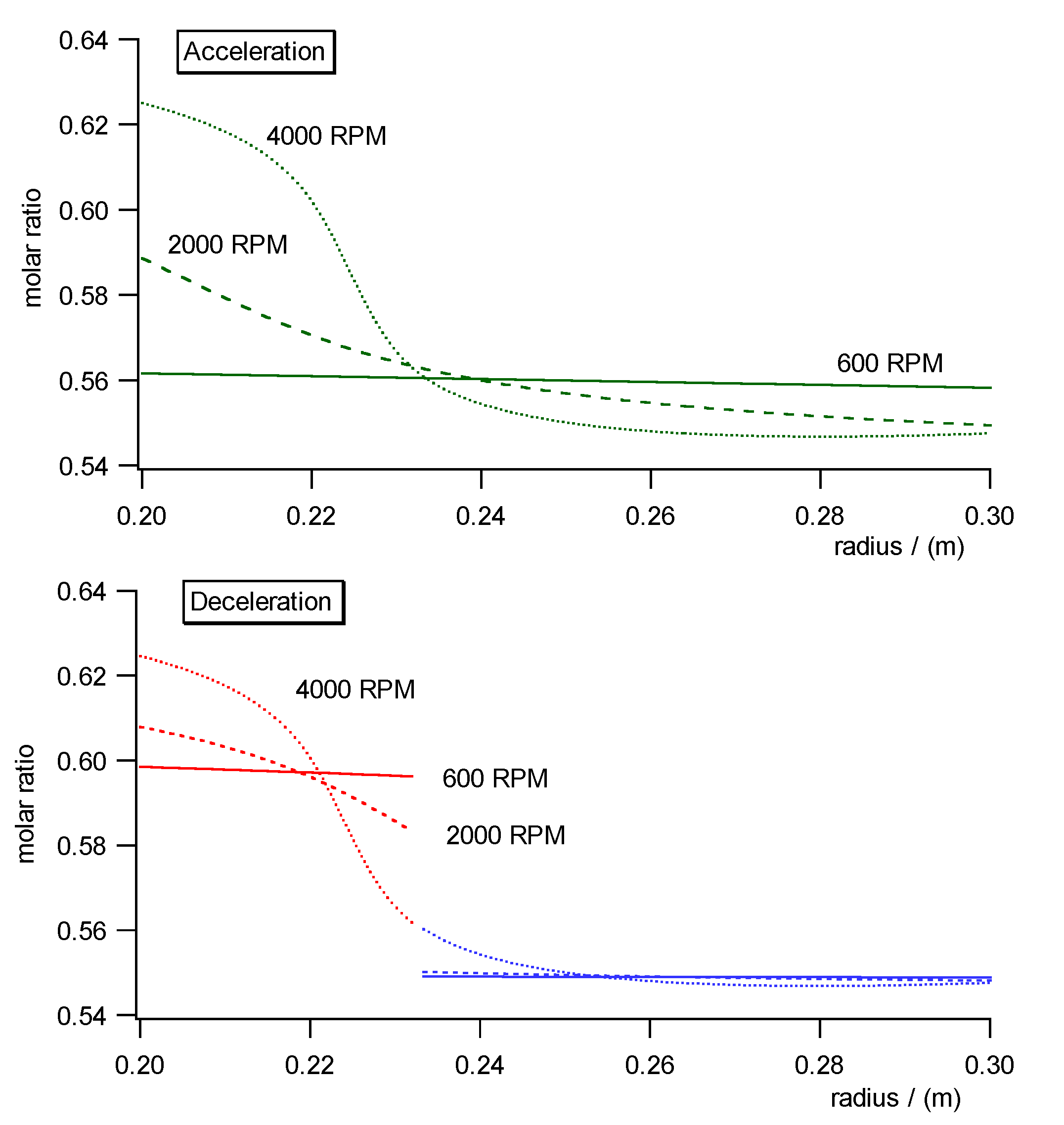Fig. 10a)- c) shows the pressure, concentration and specific molar volume profiles versus radius in the centrifugal field each during acceleration (upper diagrams) and deceleration (lower diagrams). Fig. 11 shows the work diagram of the cycle calculated from the diagrams of  Fig.10a)-c) using a tabel calculation program.
 

5.Discussion

The orientation of the isothermal cycle indicates a mechanical energy loss. This can be seen if we write down the definition of work.

If we compare fig.11 it can be confirmed that the calculated work orientation of the integral is a loss.
The difference values between up and down curve of the angular moment versus rotation speed w have a lower limit of three times of the computation error (~0.5% computation error for angular momentum).
Due to the linear "mixture rule" of molecular weight the equation of state does not change pricipally. It holds the principle of local equilibrium and the critical point of the phase diagram does not move, if a field is applied, as shown in (22).
Only mixture rules higher that linear (possible in electric fields) such effects are possible which is explained in more detail in (9).
Another perhaps more promising perspective of thermodynamic centrifugal field applications are phase equilibria in slow chemical reactions. Because chemical potentials are influenced by a field the equilibria in volume should be shifted along the coordinate under the influence of a field . Therefore, things like "new age vortex water treatment" can change the path of appropriate chosen chemical reactions, as stated long ago by Schauberger (23).
 

Appendix 1: The Poynting energy conservation reduced to a energy conversion formula

The Poynting formula is written

We neglegt the ExH term and either the electrical or magnetic field energy term.
We identify
1) the volume to integrate with the wire and write d3 r= A(r)dr.
2) CU2/2 =  E.D/2 dr3  or LI2/2 =  H.B/2 dr3  for standard capacitances or inductivities.
Then we can write for pure capacitances
and for pure inductivities












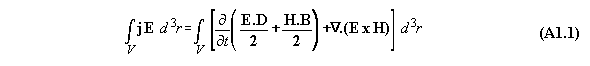
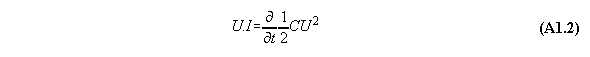
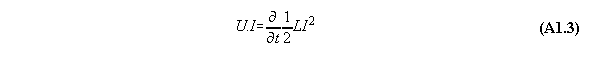
Appendix 2: Momentum conservation of a many particle system with internal central forces

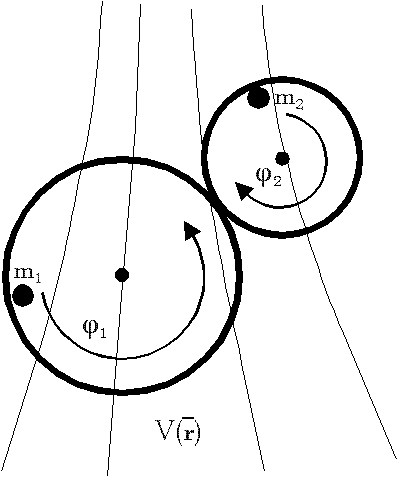
Proposition:
Inner forces do not contribute to the total momentum of a many particle system if they are central forces between the particles which can be derived from a potential.

Proof:
We assume that the force between the molecules i and j is a potential function dependent only from distance, i.e. V(ri-rj). The Hamiltonian for the whole system including inner forces is

where

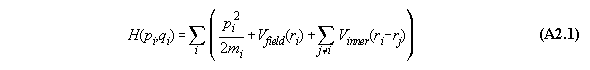
If we regard the total force on the whole system we get

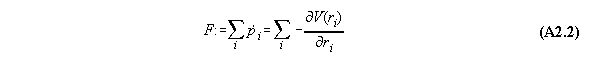
because each term of the inner force potential Vinner(ri-rj) between two particles is compensated by its counterpart Vinner(rj-ri). This is equivalent to Newton's actio-reactio law.

Appendix 3: Second variation of gravitational and centrifugal fields

A) Centrifugal field
For thermodynamic potentials including centrifugal fields holds

with  being the kinetic energy potential in the centrifuge.
If we take the second variation of this potential (i.e. the second derivation) we get minimum behavior of U´ of irreversibilities because of
and maximum behavior of U´´ due to
This behavior is analogous to the magnetic field; the angular momentum L corresponds to field B, corresponds to the current I .

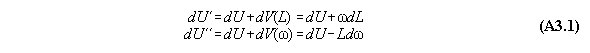
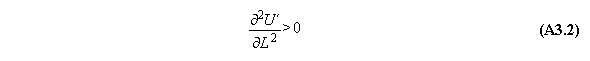
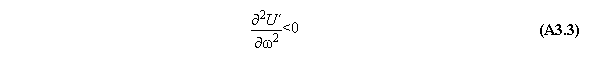
B) Gravitational field
For thermodynamic potentials including force fields like gravitation holds

with   with  being the definition of the force in the field.
If we take the second variation of these potentials (i.e. the second derivation) we get maximum behavior of U´ of irreversibilities because of
maximum behavior of U´´ as well due to












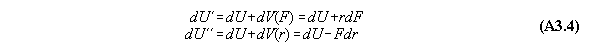
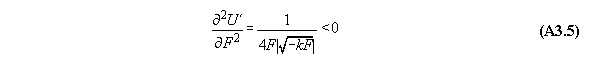
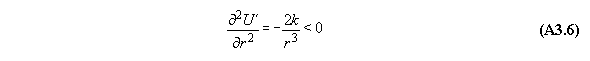
Appendix 4: The degrees of freedom of a multicomponent mixture in a potential field

In order to calculate a phase equilibrium we consider a tubular volume filled with fluid with n components in a field V(r) with the coordinate r. As an approximation the volume is divided into m compartments for calculation purposes. In each compartment the equation of state is fulfilled locally with defined values P(v(rj),xi(rj), T(rj)) and µi(v(rj),xi(rj), T(rj)), comp. fig.A4.1(last pic) .

Numbers of equations:
1) The next equation shows that the pressure equation is linearly dependent from the chemical potential equations.

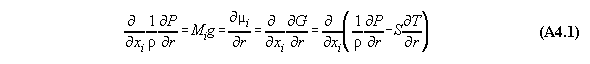
From this equation follows as well that T is independent of r, i.e. it is constant over the whole volume.

Therefore, between two adjacent compartments exist each n equations. It is recommended to take only the equations of chemical potential for calculation purposes in order to avoid integrals in the algorithm. Therefore, n.(m-1) equations (32) and (33) exist between the m compartments, indicated by the double arrows in equ. 47 !
2) Additionally we have n equations of mass conservation (see equs. 35), i.e.
 
 

In sum we have n.(m-1) + n = n.m equations.

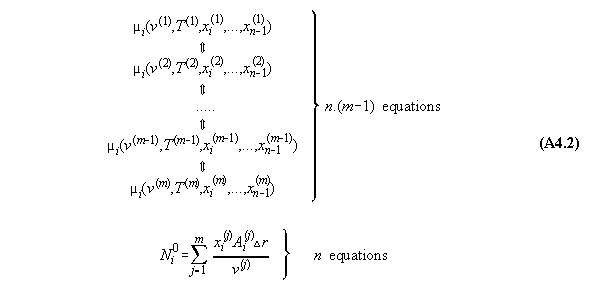
Number of variables:
Because temperature is constant over the volume we have n.m unknown variables v(m) and xi(m) over the volume.
Therefore, because the numbers of variables is equal to the numbers of equations, the system is determined completely.
 

Appendix 5: Calculation of the thermodynamic state of a real fluid with a Bender equation of state
 

Bibliography:

[1] W.H. Müller, W. Muschik J.Non-Equilib. Thermodyn. Vol.8 (1983) p. 29 - 46
Bilanzgleichungen offener mehrkomponentiger Systeme I. Massen und Entropiebilanzen (in German)
[2] W. Muschik, W.H. Müller J. Non-Equilib. Thermodyn. Vol.8 (1983) p. 47 - 66
Bilanzgleichungen offener mehrkomponentiger Systeme II. Energie und Entropiebilanz (in German)
[3] W.D.Bauer at http://www.overunity-theory.de/magmotor/magmotor.htm
Do non-conservative potential perpetual running machines exist
[4] F.Kuypers Klassische Mechanik 5.AuflageWiley-VCH 1997
[5] van Platen US patent 4.084.484 18.4.1978
[6] Bauer W.D., Muschik W. J. Non-Equilib. Thermodyn. Vol.23, No.2,1998, p.141 -158
[7] Bauer W.D., Muschik W. Archives of Thermodynamics Vol.19, No.3-4, 1998, p.59-83
[8] Bauer W.D. From mechanics to thermodynamics http://www.overunity.com/2ndlaw/2ndlaw.htm
[9] Bauer W.D. Incompatibility of Planck's Version of Second Law Regarding Mixtures in Fields http://www.overunity-theory.de/bauer/index.html
[10]V.Freise Chemische Thermodynamik BI Taschenbuch 1973 (in German)
[11] D. Wirtz, G.G. Fuller Phys.Rev.Lett.71 (1993) 2236
[12] J.U. Keller Thermodynamik der irreversiblen Prozesse, de Gruyter, Berlin, 1977 (in German)
[13] Bhattacharya K., Friesecke G., James R.D.
Proc. Natl. Acad. Sci. USA Vol.96,pp.8332-8333 1999
The mathematics of microstructure and the design of new materials
[14] Platzer, B.
Eine Generalisierung der Zustandsgleichung von Bender zur Berechnung von
Stoffeigenschaften polarer und unpolarer Fluide und deren Gemische
Dissertation Fachbereich Maschinenbau
Universität Kaiserslautern 1990 (in German)
[15]Polt, A. Zur Beschreibung der thermodynamischen Eigenschaften reiner Fluide mit
erweiterten BWR-Gleichungen Fachbereich Maschinenbau Uni Kaiserslautern 1986/87
[16] Tsai F.-N., Shuy J.-H.
Prediction of High-Pressure Vapor-Liquid Equilibria by the Corresponding-States Principle
Journal of the Chin. I. Ch. E., Vol.16,No.2, 198, p. 157-163
[17]Reid, R.C., Prausnitz, J.M., Poling, B.E. The Properties of Gases and Liquids, McGraw-Hill, New York 1987
[18] Stephan K., Mayinger F. Thermodynamik Bd.II
Springer Verlag Berlin, New York 1988
[19] Fletcher, R.
A modified Marquard Subroutine for Non-Linear Least Squares
U.K.A.E.A. Research Group Atomic Energy Research Establishment
(AERE) - R.6799, Harwell 1971
[20] Ahrendts J., Baehr H.J.
Die Anwendung nichtlinearer Regressionsverfahren bei der Aufstellung thermodynamischer
Zustandsgleichungen (in German)
Forsch. Ing.Wes. 45 1979 no.2 p.51-56
[21] Christiansen L.J., Fredenslund Aa.., Mollerup J., Cryogenics July 1973 p.405-413
[22] P. Debye, K. J. Kleboth   J. Chem.Phys.42 (1965) 3155
[23] Coats C. , Living energies - Viktor Schauberger´s brilliant work
GATEWAY BOOKS 1996 The Hollies,Wellow, Bath, BA2 8QJ, UK
in German: Naturenergien verstehen und nutzen -Viktor Schaubergers geniale Entdeckungen
Omega-Verlag, Düsseldorf, 1999
 

Tables:

Table 1: different realizations of the energy integral  f dx
 
form of energy
fi
xi
work
F := force
x := path
work
P := pressure
V := volume
heat
T := temperature
S := entropy
electricity
U := voltage
Q :=charge
magnetism
:= magnetic flux
:= -nI :=magnetic voltage
rotational kinetic energy 
L := angular momentum
w:= angular velocity
kinetic energy
p := momentum
v := velocity
chemical energy
µ := chemical potential
n := particle number

 

Table 2: different possible and postulated realizations of non-conservative force fields
 
system
parametrisation
energy form 1
energy form 2
windmill angle  "wind" field energy mechanical energy
"strange" iron ball
in magnetic field		 path x magnetic field energy mechanical energy
parametric changing inductivity time t magnetic field energy electric current
parametric changing
capacitance		 time t electric field energy electric current

 
 
 
 
 

Table 3: Overview of possible additional thermodynamic variables with potential extremum behaviour
 
field
Legendre transformation
extremum
magnetic field
+ M dH

- H dM
Minimum (if µ>0)

Maximum (if µ>0)
electric field
+ E dP

- P dE
Minimum (if >0)

Maximum (if >0)
centrifugal field
+ L d

- dL
Minimum

Maximum
gravitational field
+ r dF
 with ( F=m.g(r) )
- F dr
Maximum 

Maximum

 
 
 
 
 
 
 

Captions:


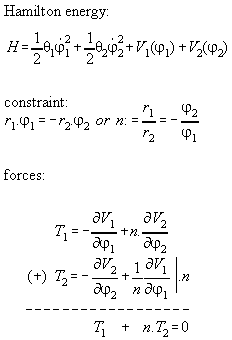Fig.1 : the comparison between experiment and theory. The connection between the variables in the theory and the experiment is done by the measurement procedure. All variables of a model must be measurable ! "hypotheses non fingo" - principle should be fulfilled on the theory side as much as possible.


Fig. 2: Illustration of the definition of a machine. It is a piece of space which exchanges different qualities like energy, momentum, mass or charge periodically balanced per definition or even founded by experiments. The volume can change periodically as well. If the complete balance cannot be found experimentally, one does not dare about if the mathematics describes the cycle correctly otherwise.


Fig.3: Illustration of an abstracted thermodynamic energy balance = 0
left pic: input work area  , right pic: output work area 


Fig.4a): water wheel totally merged in flowing water field - an example for a conservative force field exerted on the wheel. Under this conditions (i.e. symmetric coupling with resp. to by the blade resistance in the wind field) the water wheel does not turn .


Fig.4b): water wheel with lower half in a constant flow field of water - an example for a non conservative force field exerted on the wheel. The water wheel turns.


Fig.4c): wind wheel in a constant conservative laminar wind field. Due to coupling of the blades to the wind field varying with the angle  - the force field on the wheel is non-conservative. The wheel does turn.

 

Fig.5: Non-conservation of total angular momentum of a coupled particle system subjected to constraints.
The describing formulas on the right show that the total momentum    J=(T1 + T2) dt   is not conserved but instead the (unphysical and purely mathematical) entity J* := (T1 + nT2) dt . It should be noted that for this problem no periodic behavior is possible if n is a irrational number.


Fig.6a): Conservation of momentum arbitrarily dependent from the choice of the coordinate system
If the common center of mass of the planetary system is chosen as origin conservation of momentum exists.


Fig.6b): Conservation of momentum arbitrarily dependent from the system
If the fixed "sun" or "atom core" is chosen as origin of the coordinate system no conservation of momentum can be found.


Fig.7: Definition of the angular momentum of a distribution, comp. eq. 12 in text . Does make this sense ?

Fig.8: The phase diagrams of the mixture Ar-CH4 at 170 K acc. to the calculation with a Bender equation of state.
Upper diagram : Pressure versus molar ratio of Argon. Lower diagram: spec. volume versus molar ratio of Argon
Fat line represents border line between 1 and 2-phase are. Enclosed areas are 2-phase areas. Point K represents the critical point.


Fig.9: Experimental setup for the w-L - cycle in centrifugal field
a) centrifuge at no rotation w=0, equilibration of mixture  --> acceleration at lower moment of inertia
b) centrifuge at rotation w=const. heavier components go into periphery
c) same as b) but compartements are separated by closing tap  --> deceleration at higher moment of inertia
d) centrifuge at no rotation w=0, heavier and lighter components are separated now
e) centrifuge at no rotation w=0, opening the tap, mixture returns to state a)


Fig.10a): Spec. volume profile in a rotating vessel versus radius r at different rotation speeds
Initial state without field: Argon - Methane 55 bar,  molar ratio x1 Argon 0.56, temperature 170 K
vessel: inner edge r1=20cm and outer edge r2=30cm,
computation: 150 array points due to computer restrictions
volume splitting point at 4000RPM at about 0.233 m.


Fig.10b): Pressure profile in a rotating vessel versus radius at rotation speed
Initial state without field: Argon - Methane 55 bar,  molar ratio x1 Argon 0.56, temperature 170 K
vessel: inner edge r1=20cm and outer edge r2=30cm,
computation: 150 array points due to computer restrictions
volume splitting point at 4000RPM at about 0.233 m.


Fig.10c): Molar ratio profile x1 of Argon in a rotating vessel versus radius at different rotation speed
Initial state without field: Argon - Methane 55 bar,  molar ratio x1 Argon 0.56, temperature 170 K
vessel: inner edge r1=20cm and outer edge r2=30cm,
computation: 150 array points due to computer restrictions
volume splitting at 4000RPM at about 0.233 m.


Fig.11: Angular momentum versus rotation speed of a Argon - Methane mixture, calculated from the arrays of fig.10
the work diagram of the isothermal cycle with volume splitting shows a slight work loss.
Initial state without field: Argon - Methane 55 bar,  molar ratio x1 Argon 0.56, temperature 170 K
vessel: inner edge r1=20cm and outer edge r2=30cm,
computation: 150 array points due to computer restrictions
volume splitting at 4000RPM at about 0.233 m.


Fig.12: Sediments before (left pic) and after vortex water treatment (right pic) after Schauberger. Sorry, no concrete experiment description found ! :-) The cristalline structure seems to have been changed.

Fig. A4.1: Our approximation in order to calculate the phase equilibrium in a field. The volume is divided in m different array cell. As shown in the text of appendix 4 it comes out that the temperature has to be constant.