Overunity theory article

It is proved that Planck's and Clausius's version of the 2nd law contradict to Gibbs's thermodynamics if cycles of mixtures in fields are included into consideration. Experiments support the Landau-Lifshitz formulation of the 2nd law for fields which allows 100% efficiency conversion of heat into electrical work under isothermal conditions.

1)Introduction

It is well known theory that according to Gibbs's version of the second law the thermodynamic potentials go to an extremum. Gibbs's formulation is regarded as equivalent to Planck's perpetuum mobile forbidding version of the 2nd law although the complete equivalence between both formulations of the second law never have been proved generally, especially if we apply the extremum principle of the thermodynamic potentials to electromagnetic fields. In this article we will investigate this question.

2)The Second Law for Electric and Magnetic Fields

According to Landau and Lifshitz [1] the free enthalpies G' and G" of a capacitive loaded system are defined by

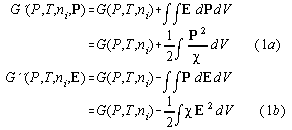
where we used the definitions =susceptibility, E= electric field, P= electric polarisation, V=volume,and P=pressure. (we omit dielectric constants of vacuum) In differential form we have

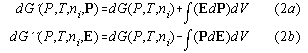
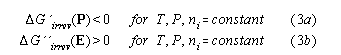
3) Isothermal Isobaric Electric Cycles of Non-Linear Dielectrics through Phase Transitions

In this section we investigate isothermal and isobaric electrothermic cycle with an intense electric field applied to a non-linear dielectric substance in a capacitor. One part of the cycle is reversible, the other is irreversible. T and P are constant (dT=0,dP=0) during the whole cycle.

It is well known that electric cycles of ferroelectrets show a loss hysteresis of electric work. Using the Landau-Lifshitz version of the 2nd law we will show that we have a hysteretic loss if irreversibilities occur in the cycle at fixed polarisation P. Therefore, touching point 1 and 2 we proceed a closed isothermal isobaric electric cycle (1->2->1) in the P-E -diagram with an irreversible part (2->1) at constant polarisation P . Because G' is a potential it holds

The second law is  G'(2->1)<0. According to our initial assumption we have P1=P2 and during the irreversible phase (2->1) of the cycle. This zero expression is added to the first line of (1a) and using formula (3a) and (4) we obtain

An analogous consideration we apply to a cycle with an irreversibity at fixed field E: Because G'' is a potential, for a closed cycle over three points(1->2->3->1), cf. fig.2, we have

According to the Landau-Lifshitz version of the 2nd law  G"irrev > 0 holds because G"irrev goes to a maximum. Because the of isofield (E2=E3) irreversible change of state(2->3) we have also . This zero expression is added to the first line of (1b) and using formula (3b) and (6) we can write

4) A possible example for violation of Planck's version of second law

As a candidate for realisation of such an effect we propose here a "splitted" isothermal cycle in fields using near critical point solutions investigated and characterized by Wirtz and Fuller [2]. They investigated electrically induced phase transitions of polymer solutions like polystyrene in cyclohexane (upper critical point solution) or p-chlorostyrene in ethylcarbitol (lower critical point solution). The closed splitted cycle is proceeded using such a sol-gel liquid dielectric substance in a capacitor. The composition of the liquid is separated periodically by a demixing phase transitions induced by switching off the field. After the separation of both phases they are remixed again (irreversible phase !) after switching on the strong field.

The cycle is started in the 2- phase region at zero field at the points 1, comp.fig. 1,2 and 3, where the volume is splitted by closing the tap separating both phases. Then a strong electric field E is applied. So we reach the points 2' and 2'' representing different phases of the solution in both compartments. Then we open the tap and let mix the solutions in both compartments. During the mixing (2->3) the electric field is kept constant by decharging the capacitor during the decline of the dieleletric constant, cf. fig.4. In the phase diagram fig. 3 from [2,6] and as well in fig. 1 +2 the mixed solution is at the phase separation line at point 3. Then doing the last step of the cycle the capacitor is decharged completely and the system goes back into the 2-phase area to point 1 and demixes. According to the theory (cf. formula (3b) and (6))

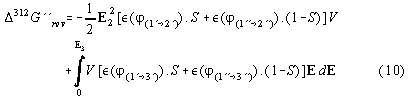
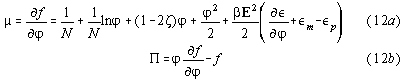
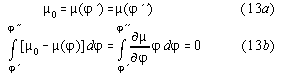
5) Conclusion

We have shown that the second law in the Planck version or in the version of the maximum entropy principle can lead to contradictions to the Gibbs formalism if the influence of fields on irreversible processes is considered. It is dependent from the path of the irreversibility in the state space whether we get a loss or a gain hysteresis of the electric work. Therefore the question arises how to reformulate the second law. Remembering that thermodynamics can be regarded as mechanics of a many-particle system reduced in the number of coordinates then it is clear that a reformulation should include mechanics as well. It is not a new idea that the second law is a consequence of the principle of least action [7] in mechanics and if we go back to Landau and Lifshitz [1] we realize that they use the variation principle as well in order to derive the electromagnetic extensions of the thermodynamic potentials from the Maxwell equations.

References:

1)L.D. Landau, E.M.Lifshitz Electrodynamics of Continous Media (Pergamon, Oxford) 1984

2)D. Wirtz, G.G. Fuller Phys.Rev.Lett.71 (1993) 2236

3)P. Debye, K. J. Kleboth J. Chem.Phys.42 (1965) 3155

4)P.G. de Gennes, Scaling Concepts in Polymer Physics (Cornell University Press Ithaca, London 1985)

5)J. Des Cloizeaux ,G. Jannink Polymers in Solution Oxford University Press Oxford 1987

6)D. Wirtz, K. Berend, G.G. Fuller Macromolecules 25 (1992) 7234

7)W.G. Hoover Phys.Lettr. A204 (1995) p.133-135

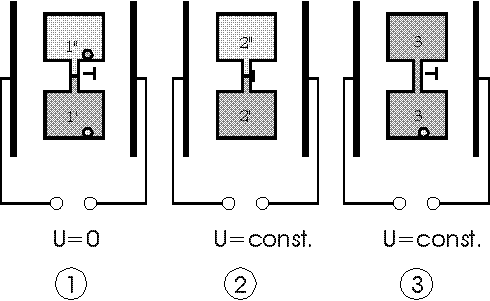
Fig 1: Isothermic isobaric electric cycle with a special polymer solution as dielectric 1) voltage U=0: system in 2-phase region 2) both volumes separated, rise of voltage from zero to U=const.: every volume part in 1-phase region 3. 3 ) voltage U=const.: opening the tap and returning to the phase separation line by remixing

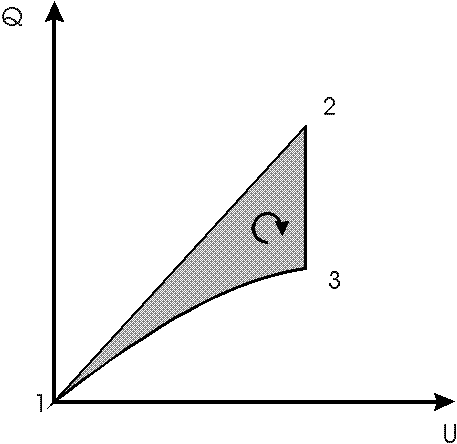
Fig.2: isothermal electric cycle in capacitor with electrically induced phase transitions; charge Q versus voltage U plotted; 1 starting at 2 phase area line with zero field, 1-2 applying a field with tap closed, 2 opening the tap, 2-3 discharging and remixing in field, 3 returning to starting point 1 by discharging the capacitor; a negative work area is predicted according to Gibbs thermodynamics contrary to Planck's version of the second law

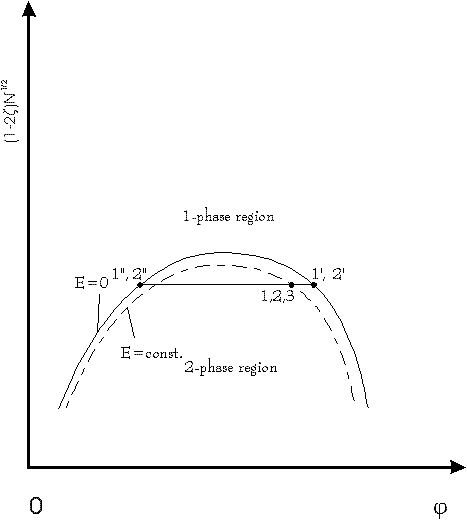
Fig.3: phase diagram of a polymer solution with and without electric field E according to [2]; plot shows modified Flory-parameter versus volume fraction of polymers; points 1: E=0, 2-phases, both points 1 at the phase separation line; points 2: E=const., both points 2 of the splitted volume in 1 phase area; point 3: E=const., after opening the tap: point 3 return exactly at the phase separation line; more information about the construction of this phase diagrams, see references [5,6]

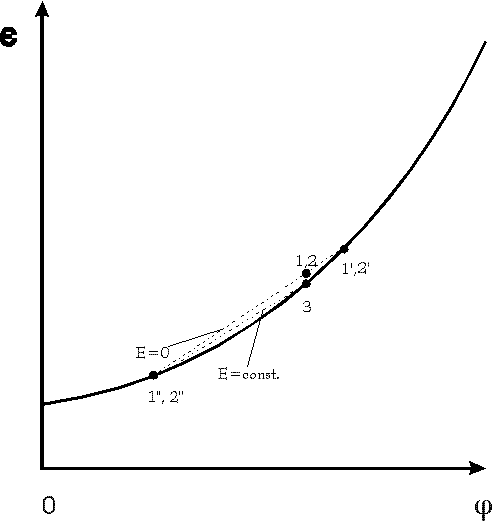
Fig.4: Dielectric constant  versus volume fraction  of polymers in a dilute solution; points 1, 2 and 3 refer to points 1-3 in fig. 1 -3. According to the theory [2,6]  holds near the critical point. Therefore  has to turn to the left and the dielecric constant has to decline during remixing 2->3. Observations at a similar system [3] support this prediction