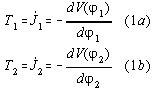
1) Introduction
Because the positive messages grow in number that there exist already
some working perpetuum mobile the question arises how this can be reconciliated
with usual physical laws. The usual killer argument of physics against
this claims is normally that all known fields can be described by potentials
fields which conserve energy during one cycle in the field. Indeed, this
argument gives a good hint where not to look for a perpetuum mobile, or
which proposals will not work. But if we have a more precise look for not
mentioned additional implicit assumptions laid down for energy conserving
potentials we see quite easily that some these machines could run indeed.
Known to the author are the following implicit assumptions which must
hold for conservation of energy and angular momentum additionally:
for angular momentum conservation:
If we have a composed system consisting of some (general) charges in
a field (i.e. mass particles in gravitational fields, magnetic poles in
magnetic field, electric charges in electric fields) the charges have to
be either independent from the neighbour charge or the they have to be
coupled to the neighbours by central forces [1].
for energy conservation:
1) the generating potential must be independent from additional variables
as parameters, i.e. especially from time .
2) Charges in conservative field which generate the conservative force
field by coupling to the field have to be constant or conserved.
We will see that if this assumptions must be dropped -because of the
mechanic design of the construction- conservation laws break down and perpetuum
mobiles become possible principally.
2) Angular moment non-conservation
It is well known fact that conservative force field do not allow any
energy gain on any closed path in a potential field. For free moving systems
angular momentum is conserved as well.However, this feature can be destroyed
if we mount general charges in a general potential field on coupled cog
wheeels or on similar working lever mechanisms. This is illustrated in
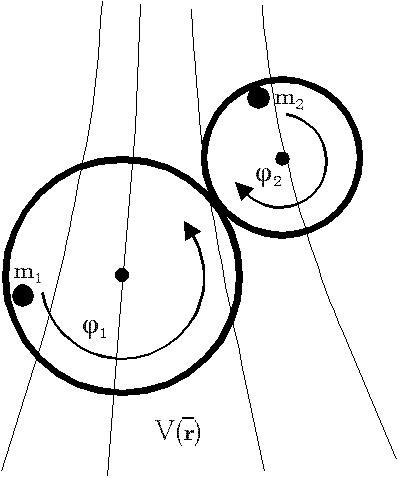
fig.1 for two charges mounted on a cog wheel each. The radiuses of the
wheel have the ratio n = r 1 /r 2 . For uncoupled
charges (no cog wheel coupling) the torques on the one-dimensional periodic
circular path of the charges can be expressed by
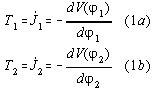
where 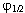 are the angle position of the charge
on the disk
are the angle position of the charge
on the disk 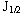 are the angular momentum,
are the angular momentum,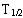 is the torque and V is the potential of the(general) force field. For coupled
wheels the equations for the torques are
is the torque and V is the potential of the(general) force field. For coupled
wheels the equations for the torques are
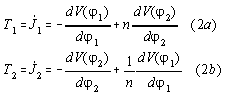
It is interesting to multiply equation 2b) by n and to add it to equation 2a). We get
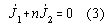
This equation represents the "conservation of angular momentum" for
this system. It is clear that this equations deviates from usual conservation
of angular momentum.
However, the energy of this system is conserved. This is case because
both equations fulfill the condition 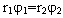 as well.
Therefore the system of equations can be written dependent only from one
variable instead of two. Therefore, because the system is only one-dimensional,
the potentials of both charges on the wheels can be obtained by integration,
the system is conservative regarding energy and allows no energy gaining
perpetuum mobile cycles.
as well.
Therefore the system of equations can be written dependent only from one
variable instead of two. Therefore, because the system is only one-dimensional,
the potentials of both charges on the wheels can be obtained by integration,
the system is conservative regarding energy and allows no energy gaining
perpetuum mobile cycles.
3) Energy non-conservation
On an official level of science there exist publications about
so called rachet potentials (periodic potential with an assymetric shape)
dependent from time which allow to gain work from noise [1.] However, the
practical application of these ideas is still at an rudimentary level.
On the other side, the newest claim of a successful perpetuum mobile
permanent magnetic design is by Greg Watson [3] who got running on a circuit
the linear patent proposal of Hartman[4]. In the meantime this design has
been successfully reproduced and works[5].
In this section we will present a simple one-dimensional mathematical
model with a space dependent ratched potential which explains the working
of Watson's SMOT,RMOD and variations therefrom quite naturally.
To get such a machine working we need
1) an assymetric shaped periodic, cyclic or linear, general potential
field ![]() (called
ratched potential) which allows to derive a general conservative vector
field E(x)= -d
(called
ratched potential) which allows to derive a general conservative vector
field E(x)= -d![]() /dx
therefrom.
/dx
therefrom.
2) a non-constant general charge q(x) dependent from path x coupling
to the field E(x)
These ingredients allow us to build a cycle which work integral can
be positive or negative depending on direction, which is indicative for
perpetuum mobile action.
We illustrate this here by a very simple mathematical model example.
We assume a charge which is dependent from x and obeys the relation
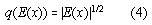
We assume a periodic ratched potential V(x) obeying the relation
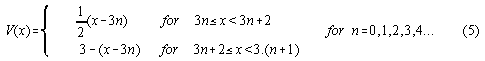
Therefrom, the field E(x) can be derived according to the definition
E(x)= -d 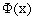 /dx of the vector field of a potential
/dx of the vector field of a potential
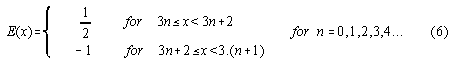
The force F(x) of the field E on the charge q is F=q.E . Therefrom, the work of one cycle can be calculated to
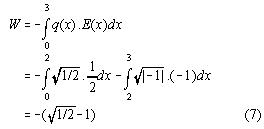
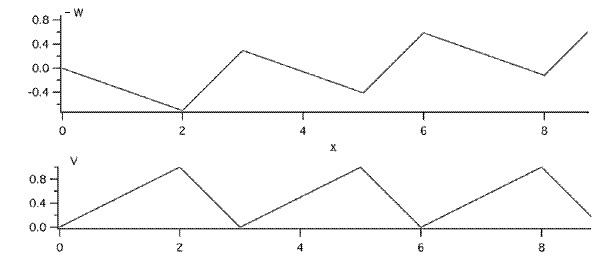
We see here that W is negativ indicating a energy gain during a cycle.
Fig.2 shows the potential 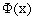 and the energy W gained
versus x. Note that if the charge is chosen constant then W=0. The same
would be probably the case if we choose a space dependent charge q(x) and
any symmetric periodic potential V during the cycle, because then both
function multiplied under the integral become symmetric and cancel to zero.
and the energy W gained
versus x. Note that if the charge is chosen constant then W=0. The same
would be probably the case if we choose a space dependent charge q(x) and
any symmetric periodic potential V during the cycle, because then both
function multiplied under the integral become symmetric and cancel to zero.
To be more practical and concrete we have to identify the mathematics
with the physics. First, we test out a case of a isotropic nonlinear magnetic
material with a unique ![]() which call the simple SMOT and which will not work -as we will see below:
which call the simple SMOT and which will not work -as we will see below:
If we move a magnetic permeable body in a magnetic field and neglect
thermic losses the formula describing the energy conversion of mechanic
energy into magnetic energy and vice versa is
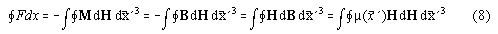
where M is the polarisation per volume element 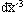 and H is the magnetic H field and B is the magnetic
B-field. The second equation holds because the added cycle integral
including the vacuum polarisation term
and H is the magnetic H field and B is the magnetic
B-field. The second equation holds because the added cycle integral
including the vacuum polarisation term 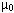 H
is zero.
H
is zero.
Now, because ![]() is symmetric resp. to H=0,
is symmetric resp. to H=0, ![]() can be written in a Taylor expansion expanded around H=0 with the
second order term as lowest order term.
can be written in a Taylor expansion expanded around H=0 with the
second order term as lowest order term.
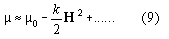
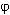 :=1/2.H2
we rewrite (8) using (9)
:=1/2.H2
we rewrite (8) using (9)
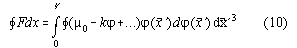
If the function in the circle integral is unique and does not depend
from other parameters the circle integral coincides with a usual integral.
Because of the periodicity of the function H(t,x') is the same before
and after a cycle of the time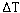 , it follows
, it follows![]() and therefore
and therefore
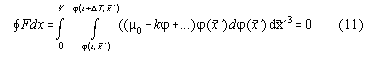
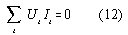
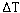
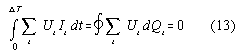
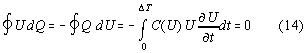
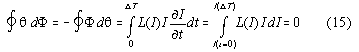
Tab.1: analogy between SMOT and electric cycles with nonlinear inductivity
and capacitance
for these system no perpetuum mobile action is possible
| system | parametrisation | energy 1 | energy 2 |
| simple SMOT | path x | magnetic field | mechanical energy |
| inductivity | time t | magnetic field | electric current |
| capacitance | time t | electric field | electric current |
Our result is contrary to the suggestion given in our last version of
this SMOT article. There we overlooked the fact that in our model substance 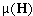 is dependent from H and not from the field
is dependent from H and not from the field ![]() which makes the big difference.
which makes the big difference.
Therefore, the question arise whether cyclic non-conservative processes
work can exist at all. We will show that the existence of cycles with overunity
efficiency depends from the question whether a material can be found whose
material constant 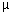 depends on a field like
depends on a field like ![]() as well.
as well.
In the most general case it holds the matrix equation ![]() as constitutive equation for any ferromagnetic material due to the field
character of the electromagnetic theory. Therefore to run a SMOT
we need
as constitutive equation for any ferromagnetic material due to the field
character of the electromagnetic theory. Therefore to run a SMOT
we need
1) material with ![]() dependent from
dependent from ![]()
2) an assymmetric ratched field H(x) from outside
Proof:
If an additional contribution due to this inhomogenity exists the formula
for ![]() can
be expanded at H=0 and we get
can
be expanded at H=0 and we get
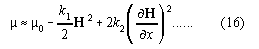
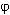 :=H2/2 ,
and using eq.(8) we get finally
:=H2/2 ,
and using eq.(8) we get finally
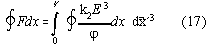
This is a expression which is nonzero for nonsymmetric periodic functions
of 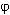 (x) in a cycle.
(x) in a cycle.
Due to the theory of ferromagnetism by Landau [8] terms of ![]() are possible for the free energy potential. These terms are attributed
to anisotropy of magnetisation caused by Bloch walls of the magnetic domains
in the bulk. At the moment the author does not see clearly whether it is
correct to apply this theory to the present problem and whether material
can be designed appropriately by making the material grains of the bulk
so very fine that the inhomogenity terms get quantitatively relevant. It
should be noted that Bruce Vandeayrs [5] SMOT contained metallic powder
as ferromagnetic material and another overunity claimed motor of Bill Mullers
motor [9] does it as well.
are possible for the free energy potential. These terms are attributed
to anisotropy of magnetisation caused by Bloch walls of the magnetic domains
in the bulk. At the moment the author does not see clearly whether it is
correct to apply this theory to the present problem and whether material
can be designed appropriately by making the material grains of the bulk
so very fine that the inhomogenity terms get quantitatively relevant. It
should be noted that Bruce Vandeayrs [5] SMOT contained metallic powder
as ferromagnetic material and another overunity claimed motor of Bill Mullers
motor [9] does it as well.
4) Conclusion
If we regard mathematics every differential equation has its own conservation
laws[10]. It is clear that real systems and consequenly its equations describing
the physics can be chosen the conservation law coinciding with the usual
conservation laws of physics. But I think I have shown that the possibility
of other choices exist as well, especially if the symmetries of fields
are broken.
Bibliography:
1) T.W.B. Kibble Classical Mechanics (second edition) p.127
Mc Graw Hill London 1973
2) Prof Hänggi's (Universität Augsburg) literature list
4) E. Hartman U.S. Patent Nr.4215330 date 29.7.1980
look at the IBM patent server
5) epitaxy@mail.localaccess.com 20.6.97 at mailing list freenrg-l at
www.eskimo.com/~billb
see as well at J.L. Naudin's
server
6) Gary's magnetic
motor
Harper's new monthly magazine March 1879, p.601-605
7) R. Unbehauen Grundlagen der Elektrotechnik 2 4.Aufl. Springer, Berlin 1994
8) L.D Landau, E.M. Lifshitz Elektrodynamik der Kontinua Vol.8
Lehrbuch der theoretischen Physik Akademie Verlag Berlin 1985
9) Gottfried Hilscher Energie für das 3.Jahrtausend VAP-Verlag Wiesbaden 1996
10) S.C. Anco, G. Bluman Phys. Rev. Lett. 78 (1997) p.2869-2873
Direct construction of conservation laws from field equations